Dvojštěrbinové experimenty v kvantové teorii
Jiří Podolský
katedra teoretické fyziky MFF UK, V Holešovičkách 2, 180 00 Praha 8
Úvod aneb století kvantové teorie
Zanedlouho, takřka současně s příchodem nového tisíciletí, uplyne již celé jedno století od chvíle, kdy Max Planck prezentoval svoji převratnou myšlenku, podle které proces vyzařování elektromagnetických vln neprobíhá spojitým způsobem. Elektromagnetické záření je tvořeno malými shluky energie a hybnosti šířícími se rychlostí světla, kvanty pole, jež dnes nazýváme fotony. Počínaje Einsteinem, který s pomocí Planckovy podivuhodné kvantové myšlenky úspěšně objasnil v roce 1905 podstatu fotoefektu, podařilo se postupně fyzikům po jistém tápání vybudovat ucelenou a vnitřně konzistentní kvantovou teorii, jednu z nejúspěšnějších teorií v historii vědy vůbec. Zásluhou kvantové teorie, tvořící spolu s Einsteinovou teorií relativity základní pilíř moderní fyziky, dokážeme dnes s nevídanou přesností objasnit bezpočet přírodních jevů počínaje chováním různých exotických částic přes vlastnosti atomů až po záření hvězd či procesy probíhající ve vesmíru bezprostředně po jeho vzniku. Souhlas předpovědí kvantové teorie se skutečností je doslova udivující. Její důsledky začínají dokonce čím dál více ovlivňovat prostřednictvím techniky i náš každodenní život - stačí připomenout například atomové elektrárny, elektroniku nebo lasery.
Komplementarita v mikrosvětě
Kvantová teorie se nám stala věrným a spolehlivým průvodcem po podivuhodné a mnohdy bizarní říši mikroobjeků. Do mikrosvěta si totiž s sebou nemůžeme jednoduše přinést klasické fyzikální pojmy a zákonitosti, na než jsme si tolik zvykli ve světě naší každodenní zkušenosti. Zejména jsme nuceni vzdáti se přirozené touhy dozvědět se o obyvatelích mikrosvěta úplně všechno. Cosi velmi tajemného a hlubokého totiž způsobuje, že naše poznatelnost přírody je zcela principiálním způsobem omezena - rozhodně mnohem více, než jsme se předtím domnívali vycházejíc z Newtonovy klasické mechaniky. Tento poznatek je dnes znám jako tzv. princip komplementarity a zformuloval jej poprvé Niels Bohr v září 1927 [1]. Podle zmíněného principu nelze mikrosoustavě bez omezení připsat současně všechny klasické vlastnosti, neboť vždy existují navzájem komplementární veličiny. Tím míníme skutečnost, že zjistíme-li pomocí fyzikálního měření přesnou hodnotu jedné veličiny, mají všechny možné výsledky měření druhé veličiny stejnou pravděpodobnost a jsou tudíž "nepředvídatelné'', neboť žádná z nich není nikterak preferována. Nejznámějším příkladem dvojice komplementárních veličin je poloha částice a její hybnost : je-li poloha mikroobjektu zjištěna naprosto přesně, pak výsledek měření její hybnosti je v souladu s Heisenbergovou relací neurčitosti zcela libovolný. Jiným příkladem komplementárních veličin jsou dva navzájem kolmé průměty spinu elektronu.
Komplementarita v mikrosvětě donutila fyziky provést kritickou revizi pojmu stav systému (viz. např. [2]). Ten je v kvantové teorii určen přesnými hodnotami všech veličin, jež se navzájem "nevylučují'', (měřením jedné veličiny není nijak narušen výsledek měření druhé veličiny), t.j. nejsou komplementární. Například kvantový stav volného bezspinového mikroobjektu i jeho vývoj je zcela určen jen jeho polohou nebo jen jeho hybností, narozdíl od klasické fyziky, v níž je stav částice určen polohou a současně hybností v daném čase. Výsledek měření ostatních (tedy nutně již komplementárních) veličin prováděných na kvantovém systému v daném stavu již není zaručen jednoznačně jistou pevnou hodnotou: lze určit pouze pravděpodobnost, s jakou danou hodnotu té které veličiny naměříme. V mikrosvětě tak byla fyzika donucena vzdáti se svých ambiciózních aspirací na možnost předpovědi toho, co se určitě stane. Napříště jí byla přisouzena pouze skromnější úloha: předpovídat, s jakou pravděpodobností cokoli libovolného v dané situaci nastane. Pochopitelně se tím podstatně změnilo i naše chápání determinismu. Je ovšem nutno v této souvislosti zdůraznit, že ačkoli se mikrosvět řídí náhodou a pravděpodobností, není zcela chaotický. Matematicky je totiž časový vývoj kvantového stavu zcela určen, a to slavnou Schrödingerovou rovnicí.
Vlnově-částicový dualismus
Snad nejznámějším a nejpřekvapivějším projevem komplementarity v mikrosvětě je tzv. vlnově-částicový dualismus. Experimentálně bylo již mnohokrát prokázáno, že tentýž mikroobjekt (například elektron, foton, neutron, atom atd.) se za jistých okolností chová jako částice, zatímco jindy se projevuje jako vlnění. Mikroobjekty "samy o sobě'' tudíž nemohou být ani klasickými částicemi, ani klasickým vlněním. Připomínají spíše novodobou reinkarnaci pradávného starořímského boha světla Janusa, neboť mají až do okamžiku měření obě navzájem komplementární tváře, vlnovou i částicovou. Kterou z nich nám při daném experimentu ukáží závisí výhradně na situaci, do níž se dostanou, t.j. na zcela konkrétním uspořádání prováděného pokusu. Je skutečností, že jakmile se začneme měřením dotazovat mikroobjektu na nějakou vlastnost typickou pro klasickou částici (například: Kterou ze dvou možných drah objekt proletěl ?), přestane se chovat jako vlna a ihned se začne projevovat jako částice. Nezáleží přitom vůbec na tom, zda si odpověď na námi položený "částicový'' dotaz opravdu přečteme, stačí pouhá principiální možnost jejího získání. Nedosti na tom ! Smazáním této "částicové'' informace způsobíme, že se mikroobjekt okamžitě začne v jistém smyslu znovu projevovat jako vlnění, a to dokonce i v tom případě, kdy experiment dávno proběhl nebo se objekt nachází velmi daleko, což by mohlo vyvolat pochybnosti o platnosti kauzality v mikrosvětě.
Zmíněné chování ukazuje, že svět kvantové teorie je vskutku podivuhodný a zdánlivě plný paradoxů. Einstein kdysi řekl, že pokud je kvantová mechanika tou správnou teorií, musí být svět bláznivý. Feynman napsal [3], že dualistické chování objektů mikrosvěta leží v samém srdci kvantové mechaniky a že v podstatě představuje jediné její mystérium. Nuže, svět má opravdu bláznivé srdce. Zásluhou nových důmyslných a technologicky náročných experimentů navržených a realizovaných v nedávných letech jsme konečně nahlédli mnohem více do hlubin jeho podstaty. Ukázalo se, že i zde kvantová teorie platí a že zmíněná bláznivost má tudiž svoji jasnou vnitřní logiku a je docela dobře pochopitelná.
Pokusy se dvěma štěrbinami
Pokusy, o nichž tu hovoříme, představují vlastně jen moderní rafinované verze klasického interferenčního Youngova pokusu se dvěma štěrbinami z počátku minulého století, který demonstroval, že světlo se při svém šíření chová jako vlnění a nikoli jako proud částic (korpuskulí), jak se domníval Newton. (Interferenci na dvojštěrbině ovšem pozoroval již F.M.Grimaldi a popsal ji ve svém díle "Fyzika světla, barev a duhy'' vydané roku 1665.)
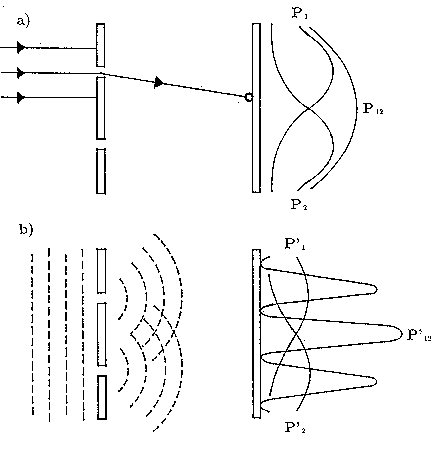
Obr.1. Schematické znázornění pokusu se dvěma štěrbinami: a) pro klasické částice, b) pro klasické vlny.
Pokus se dvěma štěrbinami je vlastně jednoduchý experiment, při němž postupně vysíláme velké množství fyzikálních objektů téhož druhu proti přepážce, v níž jsou dva podélné otvory - štěrbiny. Ty objekty, které štěrbinami projdou, jsou jimi ovlivněny a následně dopadnou na stínítko. Zde je místo dopadu každého objektu zaznamenáno. Získáme tak rozložení pravděpodobnosti, se kterou objekty na to které místo stínítka dopadají. Provedeme-li pokus s klasickými částicemi (např. s malými pevnými kuličkami), získáme rozložení pravděpodobnosti naznačené křivkou P12 na Obr.1a. Její tvar nepřekvapuje - je "hladký'' s jediným maximem na ose a je prostým součtem obou jednoštěrbinových pravděpodobností P1 a P2 popisujících situaci, kdy vždy jednu z obou štěrbin zakryjeme. Provedeme-li naopak tentýž pokus s klasickými vlnami (např. v nádobce s vodou, jejíž hladinu na jedné straně od přepážky rozvlníme a na druhé straně v místě stínítka její maximální výšku v každém bodě proměřujeme), dostaneme naprosto odlišný výsledek naznačený křivkou P'12 na Obr.1b. Křivka není v tomto případě prostým součtem obou jednoštěrbinových rozložení P'1 a P'2 . Má více maxim a minim. Hovoříme o tzv. interferenci - vzájemném "ovlivňování'' či "rušení''. Interference je způsobena tím, že se v daném místě stínítka setkávají dvě vlny od obou štěrbin v různé fázi: maximum vzniká tam, kde se setkají dva "vrcholy" vln a minimum tam, kde se setká "vrchol'' a "údolí''. Je to právě tento interferenční efekt, který ve dvojštěrbinovém experimentu odlišuje vlny od částic. Otázka po povaze objektů mikrosvěta tedy vlastně zní : naměříme při dvojštěrbinovém pokusu s nimi rozložení pravděpodobnosti s interferenčními jevy nebo bez nich ?
Velikým překvapením, které přinesly difrakční pokusy Davissona a Germera ve dvacátých letech [4], bylo právě to, že elektrony, tedy něco, co bychom si chtěli představit jako malé kuličky, budou ve dvojštěrbinovém pokusu vykazovaly interferenční jevy, což se nedávno potvrdilo i přímými experimenty. I světlo je všeobecně považováno za ukázkový příklad vlnění, které může interferovat a které se šíří prostorem, aniž by při tom zaujímalo jakoukoli konkrétní polohu.
Poznámka: S tím, jak bude postupně narůstat počet fotonů dopadlých na stínítko, bude se stále výrazněji vynořovat interferenční obrazec: proužky se objeví v těch místech, kam fotony dopadají nejčastěji. Interferenční obrazec se vytvoří i v tom případě, kdy zeslabíme intenzitu vysílaného světla natolik, že se v daném okamžiku bude v zařízení nacházet vždy jen jediný foton. To jasně dokazuje, že světlo reprezentované po dopadu na stínítko jediným fotonem (samotný dopad na stínítko totiž také znamená pro světlo jeho lokalizaci v daném místě: při dopadu se proto chová "částicově'', o čemž se můžeme přesvědčit nahrazením stínítka soustavou citlivých fotodetektorů, které budou zaznamenávat dopady jednotlivých fotonů na to které místo) nutně muselo interferovat pouze samo se sebou a projít tedy "oběma štěrbinami'' současně.
To však platí jen do okamžiku, než jeho polohu začneme experimentálně zjišťovat například umístěním dodatečných detektorů v blízkosti štěrbin. Světlo se ihned přestane chovat jako vlnění a začne se projevovat jako "částice'' - fotony: interferenční obrazec se již nebude vytvářet .
Souhrem lze říci (a veškeré doposud provedené experimenty to plně potvrzují), že v "čistém'' pokusu se dvěma štěrbinami vždy pozorujeme interferenční rozložení míst dopadu (naznačené na Obr.1b.) - mikroobjekty se v tomto případě chovají jako t vlnění, ať už jde o fotony, elektrony, neutrony, atomy atd. Jestliže však experiment navíc doplníme libovolným detektorem umožňujícím určit, kterou z obou štěrbin zkoumaný objekt prošel (t.j. získat informaci o realizované cestě), interferenční efekty zmizí a naměříme prosté částicové rozložení pravděpodobnosti dopadu (viz. Obr.1a.).
Do formalismu kvantové teorie je zmíněné chování zabudováno prostřednictvím následujících tří pravidel [3], [2]:
- 1. Pravděpodobnost P dopadu na určité místo stínítka je dána P = psi* psi kde psi je hodnota komplexní vlnové funkce v daném místě stínítka a hvězdička znamená komplexní sdružení.
- 2. Může-li proces proběhnout přes několik nerozlišitelných mezistavů (zde představovaných průchody dvěma různými štěrbinami), pak se aditivně sčítají dílčí vlnové funkce. V našem případě je psi = psi1+psi2, kde psi1 resp. psi2 jsou vlnové funkce odpovídající průchodu jen horní resp. jen dolní štěrbinou. V důsledku toho je (nenormovaná) pravděpodobnost dána P = ( psi1* + psi2* )( psi1 + psi2 ) = P1 + P2 + psi1* psi2+psi2* psi1 . Poslední dva "smíšené'' členy popisují interferenci.
- 3. Jsou-li mezistavy navzájem v principu rozlišitelné (t.j. jsme-li v experimentu schopni určit, která z alternativ mezistavů nastala), sčítají se aditivně samy dílčí pravděpodobnosti, nikoli vlnové funkce, t.j. P=P1+P2.
Einsteinova verze pokusu
Popsané dualistické chování objektů mikrosvěta v pokusu se dvěma štěrbinami je z hlediska klasické fyziky nečekané a přímo vyzývá k experimentálnímu ověřování. Byl to sám Einstein, který v roce 1927 navrhl verzi Youngova pokusu [1], od níž si sliboval, že prokáže nekonzistenci kvantové mechaniky (Einstein totiž patřil k vůbec největším kritikům této teorie).
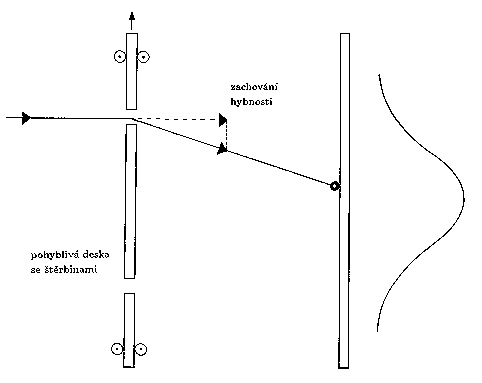
Obr.2. Einsteinova verze pokusu se dvěma štěrbinami a světlem. Může-li se přední deska pohybovat, lze určovat realizovanou dráhu fotonů a interferenční obrazec se rozmaže.
Podle Einsteina stačí uvolnit přední desku se štěrbinami tak, aby se mohla pohybovat ve směru naznačeném na Obr.2. Protože musí platit zákon zachování celkové hybnosti dopadajícího i prošlého fotonu a desky (o níž předpokládáme, že je na počátku v klidu), stačí sledovat pohyb desky po průchodu fotonu štěrbinami, abychom určili realizovanou dráhu. Pokud foton na obrázku prošel horní štěrbinou, bude se deska pohybovat směrem nahoru, prošel-li dolní, bude se pohybovat dolů. Podle Einsteina se na stínítku vytvoří Youngův interferenční obrazec a přitom jsme schopni určovat realizovanou dráhu, což je ve sporu s postuláty kvantové teorie. Jak však záhy ukázal Bohr, Einstein se ve svých úvahách dopustil chyby. Heisenbergova relace neurčitosti totiž platí i pro přední pohyblivou desku. Chceme-li proto určit dostatečně přesně její pohyb (hybnost), stává se její poloha více neurčitou. Právě tato neurčitost v poloze štěrbin způsobí rozmazání interferenčního obrazce v důsledku ztráty koherence (konstantního fázového posunutí podél obou drah v místě dopadu na stínítko) - přesně v souladu s pravidly kvantové teorie. Wootters a Zurek [5] nedávno znovu podrobně analyzovali Einsteinovu verzi pokusu se dvěma štěrbinami a ukázali mimo jiné, že interferenční obrazec se rozmazává tím více, čím přesnější informaci o pohybu přední desky a tedy i o realizované cestě získáváme. Je-li poloha desky naprosto jistá (např. při jejím upevnění), nevíme nic o její hybnosti ani realizované cestě a pozorujeme interferenční obrazec. Naopak při přesném změření hybnosti desky je realizovaná dráha již s jistotou určena, čemuž odpovídá rozmazaný "částicový'' obrazec bez interference. Mezi těmito dvěma extrémními případy ovšem existuje spojitý přechod: bezpočet situací, při nichž zjistíme pohyb desky s jistou konečnou nepřesností, v důsledku čehož má i informace o realizované cestě pravděpodobnostní charakter. Tomu odpovídá obrazec na stínítku, jenž je kombinací (superpozicí) částicového a interferenčního, a to přesně v kontrastním poměru odpovídajícímu míře informace o realizované cestě. Čím zřetelněji chceme pozorovat vlnovou povahu světla, tím více se musíme vzdát informací o jeho částicových vlastnostech.
Feynmanova verze pokusu
Jinou verzi dvouštěrbinového pokusu uvádí Feynman ve svých slavných přednáškách z fyziky [3].
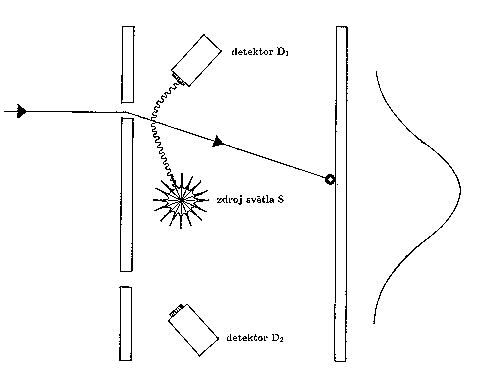
Obr.3. Feynmanova verze pokusu se dvěma štěrbinami a elektrony. Zjišťování realizované dráhy pomocí detektorů zrůsobí rozmazání interferenčního obrazce, neboť použité světlo ovlivňuje při rozptylu prolétávající elektrony.
Namísto světla (fotonů) předpokládá vysílání elektronů. Za štěrbinami je umístěn zdroj světla S, viz.Obr.3. Prolétne-li elektron horní štěrbinou, světlo se na něm rozptýlí a fotodetektor D1 namířený na tuto štěrbinu zaznamená záblesk. Naopak fotodetektor D2 zachytí záblesk jen v tom případě, kdy elektron projde dolní štěrbinou. Feynman podrobně propočítává, že i v tomto případě zjišťování dráhy elektronu pomocí fotodetektorů způsobí rozmazání interferenčního obrazce na stínítku. Je totiž třeba uvážit, že proces rozptylu světla vysílaného ze zdroje S prolétávající elektron ovlivní: světlo se při rozptylu chová jako foton nesoucí jistou hybnost a energii (nepřímo úměrné vlnové délce použitého světla). Jistá náhodná část hybnosti a energie se mezi fotonem a elektronem předá, koherence drah se poruší a interferenční proužky se rozmažou. Setkáváme se tu se situací pro mikrosvět charakteristickou: měření podstatným způsobem ovlivňuje měřený objekt. I ve Feynmanově verzi experimentu platí, že přechod mezi "částicovým'' a "vlnovým'' chováním elektronů je spojitý, a to v závislosti na vlnové délce použitého světla. Má-li světlo ze zdroje S vlnovou délku mnohem větší než je vzdálenost štěrbin, nejsme schopni rozhodnout, kterou z obou štěrbin elektron proletěl, neboť rozlišovací schopnost (přesnost lokalizace) je vždy větší než vlnová délka. Na stínítku pozorujeme ostrý interferenční obrazec, neboť hybnost a energie fotonů je natolik malá, že nemůže podstatným způsobem prolétávající elektrony ovlivnit. Zkracujeme-li vlnovou délku použitého světla, zlepšuje se rozlišovací schopnost detektorů a roste naše schopnost určit, kterou štěrbinou elektron proletěl. Současně ovšem roste hybnost i energie fotonů a v důsledku toho i poruchy způsobené v pohybu elektronů procesem rozptylu. Interferenční obrazec se rozmazává a je de facto suprepozicí čistého interferenčního a částicového obrazce v poměru daném podílem vlnové délky ku vzdálenosti štěrbin. Blíží-li se vlnová délka k nule, podávají detektory naprosto spolehlivou informaci o realizované cestě elektronů, přičemž obraz na stínítku se, v souladu s pravidly kvantové teorie, stává výhradně částicovým. Feynmanův závěr je tedy pesimistický: "Zařízení umožňující určit, kterým otvorem elektron prošel, nemůže být natolik "jemné'', aby při měření podstatně neporušilo interferenční obrazec. Nikdo dosud nenašel cestu, kterak obejít relaci neurčitosti".
Verze pokusu s "jemnou'' detekcí pomocí mikromaserů
Dnes ovšem už víme, že se Feynman v tomto bodě mýlil. Nedávno totiž fyzikové Scully, Schwinger, Englert a Walther navrhli a též uskutečnili další, tentokráte technicky velmi náročnou, modifikaci dvojštěrbinového pokusu, která umožňuje detekci realizované cesty [6]. Přínos a hloubka jejich práce spočívá právě ve skutečnosti, že jimi prováděný způsob detekce je velmi "jemný'', takže neovlivňuje rušivým způsobem měřené objekty, což bylo nedostatkem všech předchozích pokusů tohoto typu.
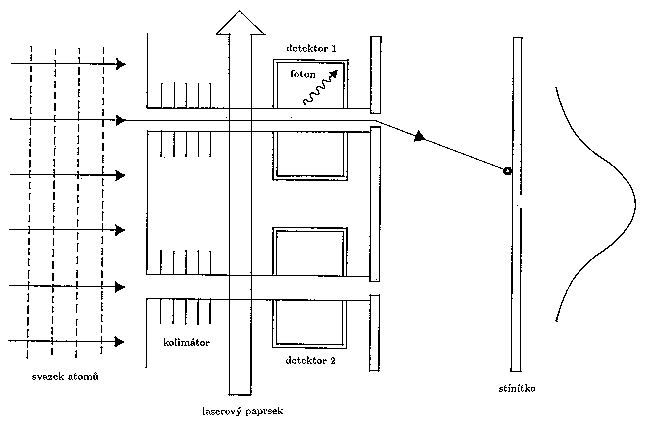
Obr.4. Zařízení, které umožňuje zjistit realizovanou dráhu atomů. Fotony vyzářené vždy v jedné z dutin jsou nízkoenergetické, takže jejich emise nenarušuje pohyb atomů.
Schematické znázornění navrženého experimentu je na Obr.4. Uvažujme proud atomů dopadající na desku se dvěma štěrbinami. Za nimi jsou umístěny kolimátory, jež vytvoří dva rovnoběžné atomové svazky. Tyto pak odděleně procházejí dvěma detektory a následně dvěma ještě užšími štěrbinami, díky nimž vznikne na stínítku obrazec. Podstata experimentu spočívá právě v použití atomů, které mají oproti fotonům či elektronům složitou vnitřní strukturu elektronových slupek a tudíž i dodatečné stupně volnosti. Právě s jejich pomocí je možno atomy "uchopit'' , t.j. nejprve "označit'' a poté vhodným způsobem detekovat. "Označení'' se provádí vhodně "naladěným" intenzívním laserovým paprskem, jenž vybudí elektrony všech procházejících atomů ze základního do vysoce excitovaného stavu, jenž má za obvyklých okolností dlouhou dobu života. Excitované atomy každého svazku v zařízení ovšem procházejí dutinami maserového detektoru, které působí jako rezonátory, kde je situace zcela jiná. Elektrony zde mají silnou tendenci přecházet zpět do stavu nižšího, v důsledku čehož vždy dojde k vyzáření nízkoenergetických fotonů. Jejich detekcí lze rozlišit, zda atom prošel horní či dolní štěrbinou. Důležité je, že fotony mají nízkou energii, a proto proces jejich vyzáření nenarušuje podstatně pohyb mnohem těžších "mateřských'' atomů.
Jedná se tedy o takřka ideální zařízení umožňující testovat základy kvantové teorie. která předpovídá, že kdykoli v zařízení získáme informaci o realizované cestě, interferenční obrazec se rozmaže. Měření provedená v Institutu Maxe Plancka v Garchingu to potvrdila. Prokázalo se, že vlnové a částicové chování kvantového systému (interference versus dráha) se navzájem vylučují. Navíc se jasně prokázalo, že to, co rozhoduje o výsledku pokusu, je samotná informace uchovaná v měřícím zařízení a nikoliv nekontrolovatelné vlivy vzniklé působením zařízení na měřený objekt. Zmíněná skutečnost implikuje vskutku "paradoxní'' možnosti spočívající v tom, že pouhou manipulací s informací o realizované cestě lze ovlivnit výsledek pokusu, a to dokonce dlouho poté, co experiment proběhl.
Problém kvantového "smazávání'' informace
Jako první upozornil na tento pozoruhodný aspekt kvantové teorie koncem 70.let J.A.Wheeler a nazval odpovídající pokusy jako tzv. experimenty s opožděnou volbou (delayed-choice experiments). Jejich podstata spočívá v tom, že experimentátor může ve dvojštěrbinovém pokusu odložit své rozhodnutí, zda bude svým měřícím zařízením zjišťovat realizovanou dráhu mikroobjektu či ne (a "donutit'' ho tím chovat se buď částicově nebo vlnově) až do doby, kdy mikroobjekt již dopadl na stínítko! Obdobně E.Jaynes [7] formuloval počátkem 80.let tzv. problémem kvantového smazávání (quantum eraser problem). Jde o to, zda je či není možné znovuobnovit interferenční obrazec prostě jen tím, že dodatečně "vymažeme'' informaci o realizované cestě uchovávanou v měřícím zařízení.
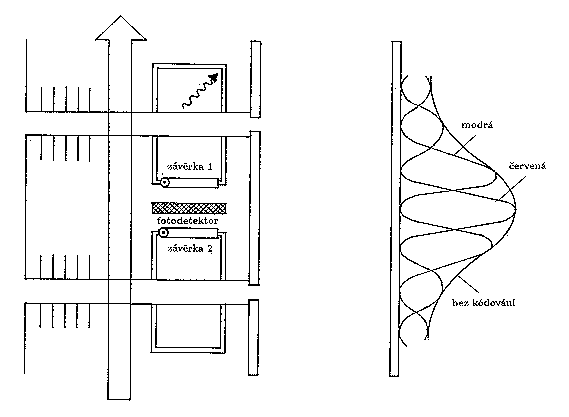
Obr.5. Modifikace pokusu umožňující testování problému "kvantového smazávání''.
Na Obr.5. je schematicky znázorněna modifikace předchozího pokusu v principu umožňující kvantové smazávání informace experimentálně provádět. Oproti zařízení na Obr.4. je zařízení doplněno jedním fotodetektorem se systémem dvou závěrek, umístěným mezi dutinami obou maserů. Na počátku experimentu jsou obě závěrky uzavřené. Excitovaný atom projde jednou z dutin (horní či dolní) a uloží zde emitovaný mikrovlnný foton, reprezentující záznam o realizované cestě. Zatímco foton rezonuje v dutině, atom projde celým zařízením a dopadne na jistém místě stínítka, kde zanechá stopu. Teprve poté otevřeme současně obě závěrky. Foton nacházející se v jedné z dutin má nyní možnost dopadnout na fotodetektor. Kvantová teorie předpovídá, že se tak stane s 50% pravděpodobností. Protože však v experimentu nejsme schopni rozlišit, zda foton dopadl na fotodetektor z horní či dolní dutiny, nepředstavuje signál z fotodetektoru informaci o realizované cestě, ale naopak skutečnost, že informace o realizované cestě (kterou bylo před otevřením závěrek ještě v principu možno získat) byla s jistotou smazána, neboť nyní již neexistuje. Stopu po dopadu atomu lze na stínítku označit barevně, a to v závislosti na signálu z fotodetektoru. Označme stopu například červeně, jestliže foton detekován byl a modře, jestliže foton detekován nebyl. Po průchodu mnoha atomů zařízením bychom podle kvantové teorie měli na stínítku spatřit interferenční obrazec složený střídavě z červených a modrých proužků, navzájem se doplňujících. Kvantová teorie tak řeší "Jaynesův paradox". Řešení spočívá právě v předpovědi (z hlediska prostého rozumu poněkud překvapivé), že fotodetektor po otevření závěrek zaregistruje foton pouze v polovině případů. Je to důsledek kvantové teorie, který nelze vysvětlit názorně (matematické vysvětlení lze nalézt např. v [6]-[8]). Ty případy, v nichž byl foton zaregistrován, vytvoří na stínítku obrazec červených interferenčních proužků, zbylé případy doplní obrazec o modré "antiproužky". Odstraníme-li barevné kódování, interferenční obrazec se stane nepozorovatelným, neboť červené a modré interferenční proužky se navzájem doplňují. To je v souladu s principem komplementerity, neboť odstranění barevného kódování efektivně znamená, že fotodetektorem měření vůbec neprovádíme (neotevíráme závěrky) a informace o realizované cestě tak zůstává neporušeně uchována v dutinách.
Uvedený příklad dává užitečný vhled do samotné podstaty problému. Ono "paradoxní" objevení se interferenčních proužků po otevření závěrek je vlastně jen pouhým rozkladem celkového obrazce do dvou disjunktních podmnožin definovaných podle toho, zda byl foton emitovaný průchodem atomu dutinami detekován či nikoli. Klíčovou roli tu hraje korelace mezi místem dopadu atomu a stavem fotodetektoru po otevření závěrek. Není to tedy tak, že by jednotlivé atomy "věděly" , kam na stínítku dopadnout dávno před tím, než jim to experimentální zařízení (a naše rozhodnutí) "řeklo". Naopak je to místo dopadu atomu, jež určuje výsledek měření fotodetektorem : pro atom dopadlý do místa červeného interferenčního proužku přejde fotodetektor po otevření závěrek do excitovaného stavu, zatímco pro atom z modrého antiproužku ne. Kauzalita zůstává i nadále v platnosti.
Měli bychom ovšem zdůraznit, že skutečná realizace pokusů schematicky znázorněných na Obr.4. a Obr.5. s "jemnou'', nedestruktivní detekcí dráhy atomů pomocí mikromaserů je technicky nesmírně náročná a leží na hranici dnešních možností. Pro zajímavost uveďme pár technických podrobností: V zařízení se nachází vždy jen jediný atom rubidia. Velmi přesně "naladěný'' laserový paprsek jej převádí do vysoce excitovaného stavu s hlavním kvantovým číslem n = 63. V dutině mikromaseru o velikosti 25mm vyrobené z niobu a chlazené kapalným heliem přeskakuje ze stavu 63p3/2 do stavu 61d5/2, čemuž odpovídá mikrovlnný foton frekvence 21,456 GHz. Příprava zmíněných experimentů proto probíhá ve špičkových laboratořích zaměřených na kvantovou optiku, především v Institutu Maxe Plancka v Garchingu. Ačkoli první předběžný výsledky jsou již k dispozici, na definitivní potvrzení odpovídajících předpovědí kvantové teorie si budeme muset ještě nějakou chvíli počkat.
Vícečásticové interferenční pokusy využívající konvertory světla
Poněkud odlišné, zato však snadněji realizovatelné verze pokusů umožňující ověřovat vlnově-částicový dualismus mikroobjektů představují experimenty využívající namísto dvou štěrbin tzv. konvertory světla ( v angličtině: down-convertors). Konvertor je v podstatě speciální nelineární krystal, který je schopen rozštěpit každý dopadlý foton vždy na fotony dva, z nichž oba mají právě poloviční energii (a tedy i frekvenci). Takto vzniklá dvojice fotonů letících různými drahami představuje z hlediska kvantové teorie koherentní dvoučásticový stav, jenž je superpozicí dvou jednočásticových stavů. Nejsou-li tyto jednofotonové stavy rozlišitelné, navzájem interferují. Pokud ovšem provádíme detekci dráhy fotonů vzniklých konverzí, interference vymizí. V takovýchto experimentech přitom interferují vždy dva fotony vzniklé v konvertoru a tím se liší od všech v tomto příspěvku doposud zmíněných pokusů, v nichž interferuje vždy jediný mikroobjekt sám se sebou.
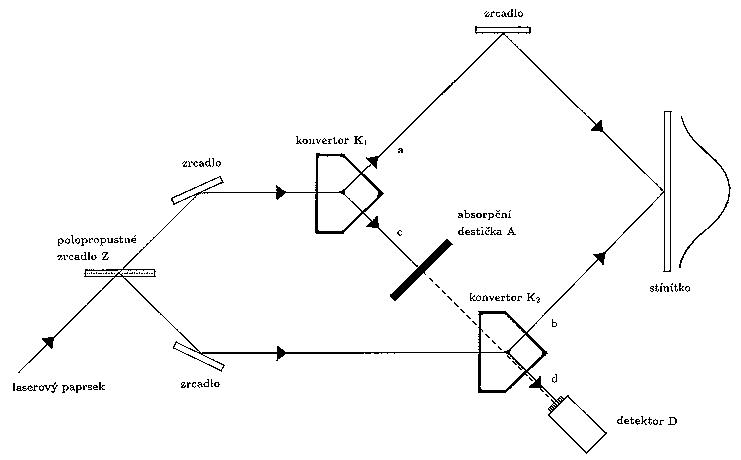
Obr.6. Verze pokusu s konvertory světla. Interferenční obrazec na stínítku se rozmaže vložením absorpční destičky A do cesty paprsku c. Míra rozmazání je úměrná neprůhlednosti destičky.
Významný experiment tohoto typu provedli v roce 1991 Mandel, Zou a Wang [9]. Schéma pokusu je na Obr.6. Laserový paprsek je nejprve polopropustným zrcadlem Z rozštěpen a oba takto vzniklé paprsky posléze odděleně dopadají na dva konvertory K1 a K2. Vzniknou tak celkem čtyři paprsky. "Hlavní'' paprsky a a b dopadají na stínítko. Zbylé dva "vedlejší'' paprsky c a d se rovněž skládají (neboť konvertor je průhledný krystal) a výsledný signál je měřen detektorem D. Takovéto zařízení neumožňuje žádným způsobem rozlišit, zda každý jednotlivý foton vyslaný laserem prošel horním nebo dolním konvertorem, a proto na stínítku pozorujeme interferenční obrazec. Světlo z laseru prochází oběma konvertory současně analogicky vlnění procházejícímu oběma štěrbinami v klasickém pokusu.
Jakmile však zablokujeme cestu "vedlejšímu'' paprsku c dodatečně vloženou absorpční destičky A, interferenční obrazec na stínítku okamžitě vymizí, rozmaže se. Změnila se totiž pozorovatelova informace o měřeném systému: experimentátor je nyní schopen jednoznačně určit, kterým konvertorem foton dopadlý na stínítko prošel. Stačí pozorovat korelaci mezi dopadem fotonu na stínítko a signálem z detektoru D: dojde-li k nim současně, foton z laseru nutně musel proletět pouze dolním konvertorem. Je dobré zdůraznit, že interferenční obrazec vymizí, i když pozorovatel nebude zmíněnou časovou korelaci měřit a zaznamenávat. Stačí pouhá potenciální možnost získání takové "částicové'' informace o dráze fotonu, aby si světlo jednu ze dvou možných drah opravdu vybralo. Mandel o tom říká: "Kvantový stav (vlnová funkce) popisuje nejen to, co o systému víme, nýbrž vše, co o něm v principu můžeme vědět''. Pro výsledek pokusu je rozhodující, co všechno může experimentátor s informací udělat, nikoli to, co opravdu udělá.
Mandel, Zou a Wang též vkládáním různě průhledných destiček namísto plně absorbující znovu demonstrovali, že míra rozmazání interferenčního obrazu na stínítku je úměrná míře potenciálně získatelné informace o realizované dráze: kontrast interferenčních proužků klesá s rostoucí neprůhledností destičky.
V posledních letech bylo navrženo a realizováno více podobných důmyslných experimentů využívajících konvertorů světla: z nich vycházející fotony jsou vždy korelované a umožňují tak ověřovat vzájemnou interferenci více částic. Na experimentech je přitažlivé především to, že ačkoli svým způsobem ověřují nejhlubší principy kvantové teorie, jejich podstata je srozumitelná a pochopitelná i pro člověka, který není odborníkem na kvantovou optiku. Popis zmíněných pokusů lze nalézt např. v [10], [11].
Závěr
Veškeré doposud provedené experimenty prokazují, že fotony, elektrony, neutrony ba dokonce celé atomy se někdy chovají jako vlny, jindy jako částice a občas jaksi "obojím způsobem''. Různé "paradoxy'' a "nepochopitelnosti'' ohledně vlnově-částicového dualismu vznikají však jen díky našemu hluboce zakořeněnému předsudku přenesenému z klasického světa, totiž že mikrobjekt má "sám o sobě'' nějakou vlastní fyzikální podobu. Stále se mylně snažíme představovat si, že mikroobjekt vypadá buď jako vlna nebo částice, že proletěl buď oběma štěrbinami nebo pouze jedinou. Ve skutečnosti však nejsou kvantové jevy ani vlnami, ani částicemi. "Samy o sobě'' zůstávají naprosto "bez tváře'', nemají žádnou klasickou podobu. Až teprve v okamžiku měření si pro nás nasazují příslušnou "masku'', a to vždy v souladu s naší volbou: zjišťujeme-li ve dvojštěrbinovém experimentu realizovanou dráhu, má maska podobu částice, nejsme-li schopni dráhu ani v principu určit, má podobu vlny. (V terminologii kvantové teorie říkáme, že nepozorovaný kvantový mikroobjekt se nachází v koherentní lineární superpozici veškerých možných nerozlišitelných stavů. Jakmile ovšem pozorovatel provede měření umožňující mezi těmito přípustnými možnostmi rozlišit, vlnová funkce je donucena zredukovat se do jednoho jediného stavu.) V tomto smyslu opravdu platí v kvantovém světě slavná věta filosofa Berkeleyho, že "býti znamená býti vnímán''. Wheeler dokonce spekuluje že fyzikální jevy jsou přímo určovány otázkami, které přírodě kolem sebe klademe, a že tudíž nejsme pouhými pasivními pozorovateli vesmíru, ale jeho aktivními účastníky, ba spolutvůrci.
Fyzikové dlouho vášnivě diskutovali, co se vlastně odehrává při vlastním procesu měření, kdy dochází k interakci "kvantového'' mikroobjektu s "klasickým'' měřícím zařízením. Einstein, Feynman a mnozí další se domnívali, že v procesu měření hraje podstatnou úlohu relace neurčitosti, de facto vyjadřující nepostižitelnou nahodilost. Zásluhou nedávných experimentů, z nichž některé byly popsány v tomto příspěvku, dnes již víme, že proces měření, při němž dochází k dekoherenci "vlnového'' chování na "částicové'', má mnohem jemnější povahu: podstatná je samotná principiální možnost rozlišení mezistavů, korelace mezi stavem mikroobjektu a stavem přístroje po provedeném měření.
Stejné pravdilo platí podle Zureka a dalších i pro velké objekty z našeho makrosvěta [12]. Ty totiž neustále interagují se svým okolím (např. obrovským počtem molekul vzduchu), což lze také chápat jako jistý specifický druh "měření''. Měřený makroobjekt předává informaci o "realizované cestě'' do svého okolí, a proto dekoheruje do jediného "klasického'' stavu. To by mohlo vysvětlit, proč u velkých objektů nepozorujeme interferenci. Makroobjekty se chovají jako částice, přestože příslušná informace je pro nás z praktického hlediska nedostupná, neboť je rozptýlena do obrovského počtu stupňů volnosti okolí objektu: informace je ovšem v principu získatelná.
Je zřejmé, že experimenty se dvěma štěrbinami a jejich moderní analogie představují přes svoji jednoduchost velice zajímavá a krásná zařízení. Proto o nich v budoucnu v odborné i populární literatuře dozajista ještě vícekráte uslyšíme.
Literatura:
[1] M.Jammer: The Philosophy of Quantum Mechanics (John Wiley, New York, 1974).
[2] J.Formánek: Úvod do kvantové teorie (Academia, Praha, 1983).
[3] R.P.Feynman, R.B.Leighton, M.Sands: Feynamanove prednášky z fyziky - 5 (Alfa, Bratislava, 1990).
[4] A.Baiser: Úvod do moderní fyziky (Academia, Praha, 1978).
[5] W.K.Wootters, W.H.Zurek: Complementarity in the double-slit experiment:Quantum nonseparability and a quantitative statement of Bohr's principle, Phys.Rev. D19, 473-484 (1979).
[6] M.O.Scully, B.-G. Englert, J.Schwinger: Spin coherence and Humpty-Dumpty. III. The effects of observation, Phys.Rev. A40, 1775-1784 (1989).
M.O.Scully, B.-G. Englert, H.Walther: Quantum optical tests of complementarity, Nature, 351, 111-116 (1991).
E.Jaynes: in Foundations of Radiation Theory and Quantum Electrodynamics (ed. A.Barut, Plenum Press, 1980).
[7] J.Podolský: Vlny versus částice aneb nové testy kvantové teorie, Vesmír, 71, 193-196 (1992).
[8] J.Podolský: Pokusy s dvojštěrbinou - nové testy kvantové teorie, Pokroky matematiky, fyziky a astronomie, 38, 87-94 (1993).
[9] X.Y.Zou, L.J.Wang, L.Mandel: Induced coherence and indistinguishability in optical interference, Phys.Rev.Lett. 67, 318-321 (1991).
L.J.Wang, X.Y.Zou, L.Mandel: Induced coherence without induced emission, Phys.Rev. A44, 4614-4622 (1991).
[10] D.M.Greenberger, M.A.Horne, A.Zeilinger: Multiparticle interferometry and the superposition principle, Physics Today, 22-29, August 1993.
[11] J.Horgan: Quantum Philosophy, Scientific American, 72-81, July 1992.
[12] W.H.Zurek: Environment-induced superselection rules, Phys.Rev. D26, 1862-1880 (1982).
E.Joss, H.D.Zeh: The emergence of classical properties through interaction with the environment, Z.Phys. B59, 223-243 (1985).
Zpracováno podle autorova příspěvku ve sborníku semináře "Filozofické otázky matematiky a fyziky", Jevíčko, srpen 1994
Editoři J.Bečvář, E.Fuchs, D.Hrubý, A.Trojánek, JČMF, Brno 1995
