Matematika černých děr stručně

25.08.2013 14:18

Černé díry jsou předpovězené Einsteinovou teorií obecné relativity. V nejjednodušším případě jsou popsány tzv. Schwarzschildovou metrikou, což je nejstarší a nejjednodušší exaktní řešení Einsteinových rovnic. Bylo objeveno Karlem Schwarzschildem v roce 1915. Toto řešení popisuje zakřivení prostoročasu v okolí nerotujícího sféricky symetrického objektu, přičemž jeho metrika je

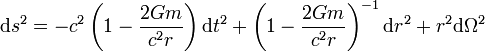
\mathrm{d}s^2 = - c^2 \left( 1 - {2Gm \over c^2 r} \right) \mathrm{d}t^2 + \left( 1 - {2Gm \over c^2 r} \right)^{-1} \mathrm{d}r^2 + r^2 \mathrm{d}\Omega^2

kde 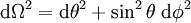\mathrm{d}\Omega^2 = \mathrm{d}\theta^2 + \sin^2\theta\; \mathrm{d}\phi^2   je standardní člen prostorového úhlu obdobný sférickým souřadnicím.

Podle Schwarzschildova řešení se kulově symetrický objekt nevyhnutelně zhroutí vlivem své vlastní gravitace do černé díry, je-li jeho poloměr menší než vzdálenost známá jako Schwarzschildův poloměr. Pod tímto poloměrem je prostoročas tak silně zakřivený, že se každý světelný paprsek vyzářený z této oblasti libovolným směrem bude pohybovat do středu celého systému. Ve středu se vytvoří gravitační singularita, oblast s teoreticky nekonečnou hustotou. Oblast pod horizontem událostí však již ve Schwarzschildových souřadnicích nelze popsat a užívá se např. Kruskal-Szekeresových souřadnic.

Schwarzschildův poloměr ve výše zavedených souřadnicích je vyjádřený jako 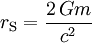r_{\rm S} = {2\,Gm \over c^2}  , přičemž G je gravitační konstanta, m je hmotnost objektu a c je rychlost světla. Pro objekt s hmotností Země je Schwarzschildův poloměr 9 milimetrů.

Střední hustota Schwarzschildova poloměru se zmenšuje se zvětšováním hmotnosti černé díry, takže černá díra s hmotností Země by měla hustotu 2×1030 kg/m³, ale supermasivní díra s hmotností 109 hmotností slunce by měla hustotu okolo 20 kg/m³, což je méně než hustota vody. Střední hustota je dána jako

 

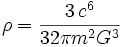
\rho=\frac{3\,c^6}{32\pi m^2G^3}

 

Vzhledem k tomu, že střední poloměr Země je 6371 km, musel by být její objem zmenšený 4×1026 krát, aby se zhroutila do černé díry. Pro těleso hmotnosti Slunce je Schwarzschildův poloměr přibližně 3 km, což je o mnoho méně než je současný poloměr Slunce. Je také mnohem menší než poloměr, do kterého se Slunce nakonec smrští po vyhoření svého nukleárního paliva, což bude několik tisíc kilometrů. Hmotnější hvězdy se však můžou zhroutit do černé díry na konci své existence.

Obecně jsou černé díry předpovídané i jinými řešeními Einsteinových rovnic, jako například Kerrova metrika pro rotující černé díry, které mají prstencovou singularitu. Reissner-Nordströmova metrika popisuje elektricky nabité černé díry. Nejobecnější řešení má Kerr-Newmanovu metriku a odpovídá případu nabitých rotujících černých děr.

 

Zpět